Functions
Functions are components of DEX models that define the aggregation aspect of alternatives’ evaluation. For each aggregate attribute Y, whose descendants in the tree of attributes are X1, X2,…, Xn, the corresponding function f defines the mapping:
f: X1 × X2 × … × Xn —> Y
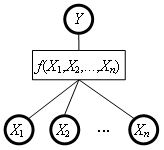
There are two types of functions used in DEX models: aggregation and discretization functions.
Aggregation Functions
Aggregation functions are the most common function type used in DEX models. They are used in cases where both Y (aggregate attribute) and all its descendants Xi are qualitative, i.e., associated with qualitative scales.
An aggregation function maps all the combinations of the lower-level attribute values into the values of Y. The mapping is represented in a decision table, where each row gives the value of f for one combination of the lower-level attribute values. Rows are also called decision rules, because each row can be interpreted as an if-then rule of the form:
if X1 = value1 and X2 = value2 and … and Xn = valuen then Y = value (or value interval)
The size of decision tables (number of elementary rules) raises quickly with the number of descendants Xi and the number of qualitative values they can take. This is known as a combinatorial explosion and should be considered carefully when designing the tree of attributes.
Particularly when decision tables are large, it is important to represent them in more compact and comprehensible forms. This includes representations using weights, which are also important in the acquisition of decision tables.
Discretization Functions
Discretization functions map numeric to qualitative attribute values. They can be associated with Y only when Y is an aggregate attribute that has exactly one numeric descendant X, so that f: X —> Y and Y = f(X).
A discretization function is defined as a collection (table) or discretization rules of the general form:
interval of X values —> single value or interval of Y
Intervals on the left hand side are defined by their corresponding lower and upper bounds. Considering the whole discretization table, the admissible bounds are constrained so that intervals cover the whole numeric range without overlapping.