Creating and Editing DEX Models
In the DEX-model creation stage, the main task is to develop an operational model. The main challenges addressed in this stage are how to
define the model and its components,
modify, edit, and maintain the model,
verify the model and its components, e.g., for completeness and consistency,
deal with uncertainty of knowledge and modeled phenomena, and
ensure transparency and comprehensibility of the model.
DEX models are typically developed by individual decision makers or groups. In most cases, DEX models are developed through expert modeling, i.e., “handcrafting” model components and structure, following the approach of expert systems. In this process, DEX models do not only “grow” from the scratch, but are often changed in other ways: attributes are added or deleted, their scales and aggregation functions are defined or changed, attribute hierarchies are restructured, etc. For all such operations, DEX Software provides interactive editing software, such as DEXi or DEXiWin.
With regard to making the model structure, a DEX editor implements all operations, mentioned above, including model restructuring through drag-drop, duplicate, and copy-paste operations. All these operations are entirely up to the user, who is responsible for the appropriate definition and selection of attributes and their connection in a feasible structure.
However, there are two model creation stages that largely benefit from an active, dynamic support of the software:
Acquiring Decision Tables and Decision Rules
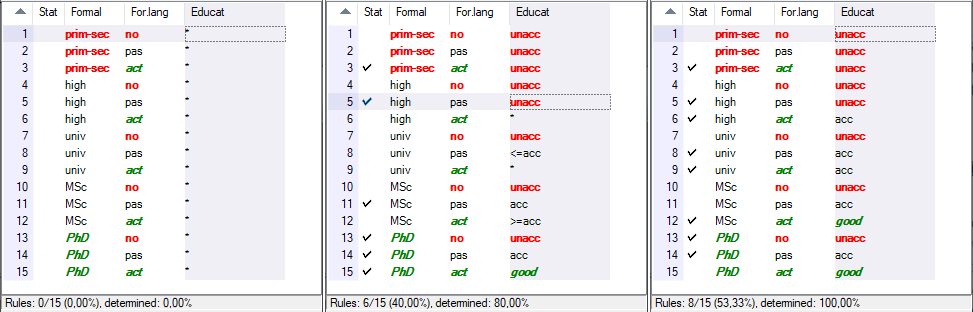
The above figure illustrates typical stages of creating a DEX aggregation function - in this case, function Educat from the Employee Selection model.
At the beginning, DEX software generates all possible combinations of values of Formal and For. lang. There are 15 such combinations, referred to as decision rules, for which the value of Educat should be determined. All the right-hand values are denoted ‘*’, representing the whole value set of Educat and effectively indicating that nothing is known about the corresponding input value combinations. The status bar below confirms than 0 of 15 rules have been defined and the function has been determined 0%.
While it is in principle possible to proceed sequentially through the 15 rules and define the value of Educat for each of them, it is usually better to follow some strategies. The example above illustrates the use scale orders strategy: defining just a few key decision rules and leaving the rest to DEX to determine using the principle of dominance. In the middle table, the user has defined 6 rules (marked with ‘✓’), clarifying the boundary requirements for ‘unacc’, ‘acc’ and ‘good’ Educat. With 6 defined rules, the function became 80% determined, leaving some incompletely defined values at rules 6 (‘*’), 9 (‘*’) and 12 (‘>=acc’). This incompleteness was resolved by defining two more rules, as shown on the right.
Handling Non-Entered Function Values
So, how does DEX method handle incompletely defined functions and determine function values that have not been entered by the user?
In DEX, function values are either entered (marked ‘✓’) by the user or non-entered. Entered values are never changed by DEX algorithms. Non-entered values, on the other hand, are handled by DEX with the purpose to aid and simplify the function editing process, and maintain the consistency of function definitions. Non-entered values are recalculated whenever the table changes. The calculation is based on already entered values and other available information (particularly scale order, and weights).
DEXi uses two strategies for calculating non-entered values, which can be individually activated or deactivated: Use scale orders and Use weights. Both are available only when function arguments are preferentially ordered attributes.
Scale orders
This strategy takes into account the ordering of scales, considering the principle of dominance. In short, when comparing two decision rules, of which the second has all the left-hand side values equal or better that the first’s, the value of the second rule should be equal to or better than the first.
Consider the function y=f(x), where both y and x have ascending scales. Then, whenever x increases, it is clear that f(x) should also increase or remain constant. This function property is known as monotonicity. A function is called consistent when all transitions between comparable rule pairs are monotone.
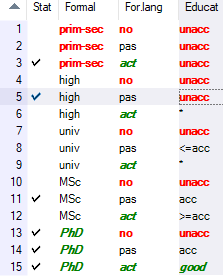
It is easy to see that, in general, monotonicity narrows the intervals of values that can be assigned to non-entered decision rules. Consider the rule 12 above. Its conditional part is Formal = ‘MSc’ and For. lang = ‘act’. The lower bound, ‘acc’, of rule 12 is constrained by rule 11, which has the same input value of Formal, but a worse value of For. lang = ‘pas’. Rule 15, with Formal = ‘PhD’, defines the upper bound ‘good’. Consequently, the interval of rule 12 is narrowed to ‘acc:good` = ‘>=acc’, as shown in the table.
This strategy fails whenever the user enters values that violate monotonicity and therefore the function becomes inconsistent. When the user attempts to enter a violating (“inconsistent”) value into a monotone rule set, a DEX editor issues a warning and requests confirmation. In the case that the user confirms such entry, the scale order strategy is deactivated.
Weights
This strategy calculates the values of non-entered rules using a hyperplane (linear function), which is constructed using weights, defined by the user, and other already entered rules. The hyperplane is constructed so that its slopes correspond to weights required by the user, and that its surface lies as close as possible (in the least squares sense) to the already entered values.
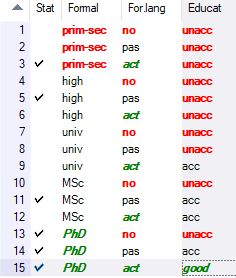
Above, the requested weights were 70% for Formal and 30% for For. lang. Using these weights and the already defined rules 3, 5, 11, 13, 14, and 15, whose values are never changed in this process, the software determined all values of the remaining decision rules.
When using this strategy, at least a few rules have to be entered by the user before this method could construct a hyperplane. The exact number of needed rules depends on function dimensions and geometric positions of entered rules, but until this condition has not been met, the strategy use weights is disabled.
Function Status
While editing a function, it is recommended to observe its status. A function is completely undefined at first: all function values contain the undefined value ‘*’. Then, values are assigned to more and more rules and the function becomes more and more defined. Usually, the goal is to completely define the function, that is, to precisely specify values for all decision rules in the table.
Two measures of function definition are used, which are both displayed as status/progress indicators.
The first measure is called entered rules ratio. This is a ratio between the number of entered rules (that is, values defined by the user) and the total number of rules.
The second measure, determination, is somewhat more complex, but usually more informative. It takes into the account that, in general, rule values are intervals rather than single values. A rule is 100% determined if it is assigned a single value, and is 0% determined if it is completely undefined, that is, it contains the complete interval of values (denoted ‘*’). For smaller intervals, intermediate values are calculated proportionally.
A function is fully determined when all its rules - both entered and non-entered - are 100% determined. This is in general achievable with less than 100% entered rules due to DEX’s handling of non-entered values. Therefore, when editing a function, the primary aim is to make it 100% determined, regardless on the proportion of entered rules.
Model Restructuring
Model restructuring is an essential dynamic property of DEX that automatically adapts a DEX model to changes and simplifies its maintenance.
At the beginning, when developing model structure, there is not much to adapt to; attributes are created, grouped in subtrees, moved around, deleted, etc. However, other model components are added later in the process: scales, functions, and alternatives. After that, any change of model structure or scale definitions may substantially affect associated functions and alternatives.
Here, DEX tries to, whenever possible, preserve as much information as possible. This is not always possible, for instance when adding or deleting function arguments, but some scale-editing operations do allow preserving function definition to some extent. Let us show an example of adapting function Educat from the Employee Selection model to deleting the value ‘univ’ of attribute Formal.
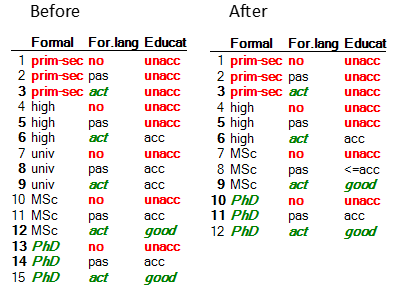
Notice that the majority of decision rules have been preserved, and only rule 8 became somewhat less defined given its new lower (rule 5) and upper (rule 11) bounds. Also note that this change affected the description of alternatives (employee candidates) behind the scene, removing all occurrences of the value ‘univ’.