Combinatorial Explosion

Consider an aggregation function f that maps the values of the attributes X1, X2,…, Xn to values of aggregate attribute Y.

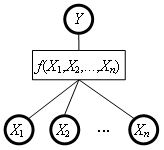
Function Y=f(X1,X2,...Xn)

In DEX, an aggregation function maps all the combinations of the lower-level attribute values into the values of Y. Suppose that each Xi has a qualitative scale consisting of si values. Then, the number of combinations and thus the size of the corresponding decision table is equal to

S = s1 × s2 × … × sn

Example

Let all the n lower-level attributes have s-valued scales. In this case, the size of f equals to

S =sn

The following table shows how fast S grows with the increasing n and s.

S=s^n

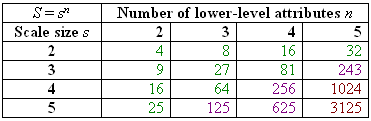
Recommendations

Experience indicates that aggregation functions of size up to 25 are small and usually quite easy to define. The difficulty grows towards the size of about 100, which is already quite difficult. Everything above 100 is very difficult, and everything above 500 is extremely hard if not impossible to define.

Also, it is not only the size that matters. The more the attributes, the more difficult the function to define, even if the size of the functions is comparable. Combining four attributes usually appears harder than combining three.

For these reasons, the DEXi method strongly advises to limit the number of aggregate attributes’ descendants to three, and to restructure the tree of attributes whenever this condition has not been met. Or alternatively, the number of decision rules in a single decision table should be kept below 100.

Restructuring Tree of Attributes

In order to avoid combinatorial explosion, it is strongly advised to structure the tree of attributes so that each aggregate attribute has only two or three immediate descendants. Whenever you encounter an aggregate attribute with four descendants, you may want to consider restructuring the tree below that attribute. Usually, there are several ways to do that:

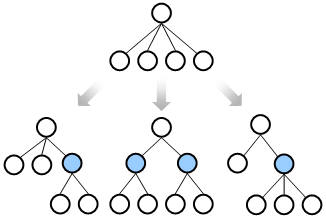
Restructuring Tree of Attributes

In all cases, you should regroup the lower-level attributes and introduce one or two new aggregate attributes. Usually, the ‘right’ structure is the one that appears the most ‘logical’, so that:

  • it groups together similar or related attributes, and

  • it is easy to give names to the newly created attributes.