Tree of Attributes

In a multi-criteria model, attributes are organized hierarchically into a tree of attributes. A model can have one or more root attributes. Each attribute can be ‘decomposed’ into one or more descendant attributes that appear one level below that attribute in the tree. ‘Decomposed’ attributes are called aggregate attributes. Attributes that do not have descendants and appear as leaves of the tree, are called basic attributes.

Interpretation

A tree of attributes can be interpreted in three ways:

1. Decomposition: It represents a decomposition of a decision problem into sub-problems. To solve ‘a problem’, which is represented by a a higher-level attribute, one has to solve sub-problems represented by its lower-level descendants.

2. Dependency: A higher-level attribute depends on its immediate descendants in the tree. This dependency is modeled by a function that is associated with the higher-level attribute.

3. Aggregation: Tree structure defines the bottom-up aggregation of alternative values. The value of a higher-level attribute is calculated as an aggregation or discretization of the values of its immediate descendants in the tree. Again, this aggregation is defined by the corresponding function.

Attributes can have the following roles:

• basic attributes represent inputs of the model,

• root attributes represent its main outputs, and

• other aggregate attributes represent intermediate results of alternative evaluation.

Example

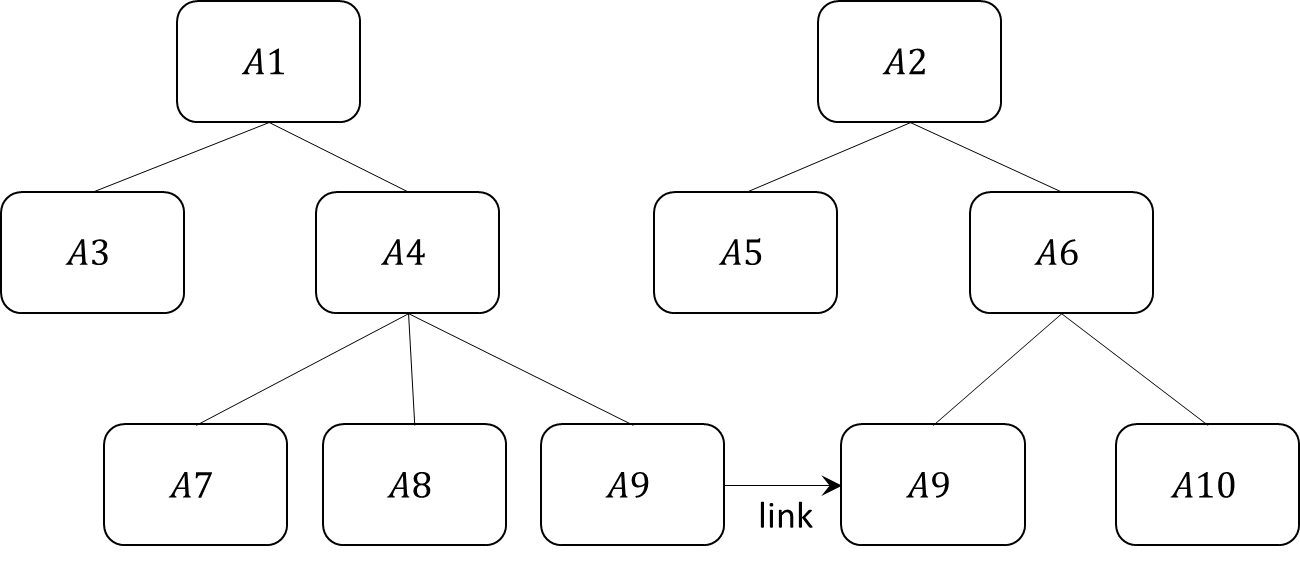
This is an example of a tree of attributes. It consists of 7 basic attributes (A3, A5, A7, A8, A9 (twice), A10) and four aggregate ones (A1, A2, A4, A6). Among the latter, A1 and A2 are two roots. The two basic attributes named A9 illustrate the concept of linking: although they appear as two separate attributes in the tree, they have the same name and have been linked together, so that they, in a logical sense, represent a single basic attribute that affects two parent attributes, A4 and A6.

Recommendations

1. Before making a real tree, create an unstructured list of attributes. Brainstorm! At this stage, try not to overlook important attributes, but do not bother about their structure or redundancy. Sketch tree structure on paper.

2. When making a structure of attributes, create meaningful subtrees that contain related attributes. Try structuring your unstructured list in two directions:

   • Bottom-up: Group similar attributes together into a single higher-level attribute. It is usually a good indication if you can find a meaningful name for it.

   • Top-down: Decompose complex attributes into simpler ones.

3. Avoid meaningless, redundant, duplicate, inessential and unoperational attributes. In other words, check each basic attribute that:

   • it has a well defined meaning,

   • it does not duplicate or overlap with some other attributes,

   • it does affect the decision (and you know how, at least approximately),

   • it can be measured or assessed with sufficient accuracy.

4. Avoid aggregate attributes that have too many descendants (usually more than three, but this depends on the size of associated scales, too). Too many descendants cause a combinatorial explosion on the size of corresponding functions, making them difficult to handle. In this case, try to restructure the tree below that attribute.