Weights
Weights are commonly used in Decision Analysis to model the importance of attributes. Weights are numbers, usually normalized to the sum or maximum of 100, which define the contribution of the corresponding attribute to the final evaluation. In Decision Analysis, utility functions are commonly defined using some form of the weighted sum, for example:
f(X1, X2,…, Xn) = w0+ w1×X1 + w2×X2 + … + wn×Xn
Here, wi denote weights and Xi denote attributes.
In qualitative multi-attribute models, there is natively no room for weights: attributes are symbolic and utility functions are defined by decision rules. However, to bridge the gap between qualitative and quantitative models, it is possible to introduce weights - in a very approximate and imprecise way - also into the qualitative models.
Principle
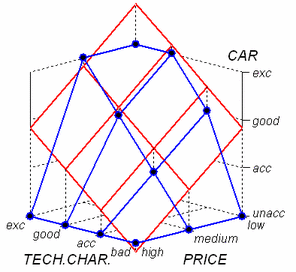
The figure above illustrates the basic approach. It shows the CAR utility function, represented by points (blue dots) in a three-dimensional space. Each point represents one defined decision rule. To find out the weights, DEXi places a (hyper)plane (shown in red) into this space so that it matches the points as closely as possible (using the least squares measure). Once done, weights can be determined directly from the slopes of the hyperplane: the higher the slope in the direction of an attribute, the higher the corresponding relative weight. In the above figure, the weights of PRICE and TECH.CHAR. are almost identical, 53 and 47, respectively. These are local normalized weights (see the definition below).
DEXi uses weights for two purposes:
as an approximate representation of utility functions, used primarily for verification and overview (see examples from the Car Evaluation model), and
for defining utility functions or their parts (see the weight-based strategy of handling non-entered function values.
Weight Types
Actually, DEXi uses four types of weights, as illustrated with the following weights from the Car Evaluation model:
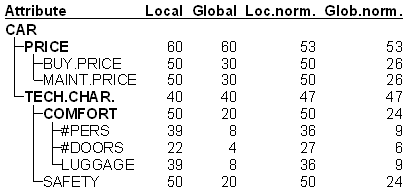
The difference between local and global is due to the tree of attributes. Local weights always refer to a single aggregate attribute and a single corresponding utility function, so that the sum of weights of the attribute’s immediate descendants (function arguments) is 100%. Global weights, on the other hand, take into account the structure of the tree and relative importance of its sub-trees. A global weight of an attribute is calculated as a product of the local weight and the global weight of the attribute that lies one level above. A global weight of the root attribute is 100%. For example: the global normalized weight of BUY.PRICE is 50% (its local normalized weight) × 53% (global normalized weight of PRICE), which gives 26%.
Weights can also be normalized or not. This is because some scales can have more values than the others. Geometrically, larger scales appear longer, they have lower slopes and, consequently, smaller weights. Normalization refers to the procedure in which all scales are adjusted to the same length (unit interval) before determining the weights. Usually, this is the better method of weight assessment and comparison of attributes.