Combinatorial Explosion

Consider a utility function f that maps the values of the attributes X₁, X₂,…, X_n into the value of the aggregate attribute Y.

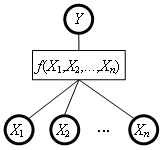
In DEXi, a utility function maps all the combinations of the lower-level attribute values into the values of Y. Suppose that each X_i has a scale consisting of s_i values. Then, the number of combinations and thus the size of f is equal to

S = s₁ × s₂ × … × s_n

In other words, when defining f, you should define S decision rules.

Example

Let all the n lower-level attributes have s-valued scales. In this case, the size of f equals to

S =sⁿ

The following table shows how fast S grows with the increasing n and s.

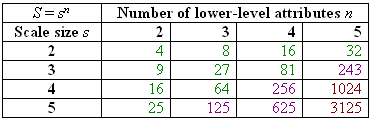
Recommendations

Experience shows that utility functions of size up to 25 are small and usually quite easy to define. The difficulty grows towards the size of about 100, which is already quite difficult. Everything above 100 is very difficult, and everything above 500 is extremely hard if not impossible to define.

Also, it is not only the size that matters. The more the attributes, the more difficult the function to define, even if the size of the functions is comparable. Combining four attributes together usually appears quite a hard task for human brain.

For these reasons, the DEXi method strongly advises to limit the number of aggregate attributes’ descendants to three, and to restructure the tree of attributes whenever this condition has not been met.

To prevent the combinatorial explosion, the DEXi program issues a warning before creating a function of size 200 or more, and disallows the creation of functions larger than 1000.